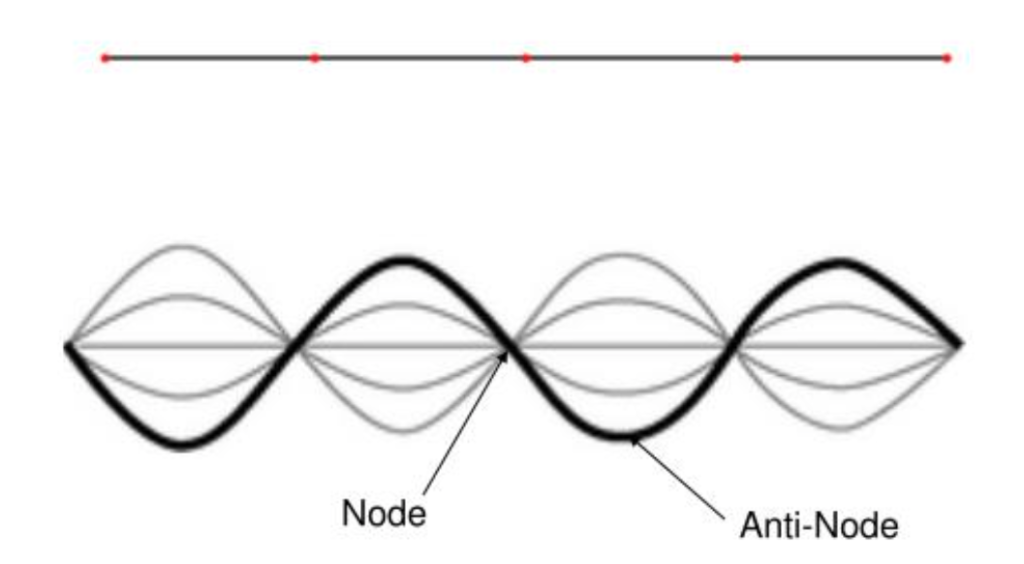
Les ondes stationnaires sont un concept important de la physique quantique. Elles permettent de décrire un grand nombre de phénomènes que les physiciens avaient du mal à expliquer de manière classique. Il s’agit notamment du rayonnement du corps noir mentionné plus haut ou de l’orbite des électrons. Bien qu’il soit trop compliqué d’expliquer ici comment elles sont exactement utilisées en mécanique quantique, le concept général et la raison de leur importance peuvent être expliqués. Tout d’abord, le concept général des ondes stationnaires est relativement facile à comprendre. Lorsque vous avez une corde et que vous envoyez une onde le long de celle-ci, elle finit par être réfléchie. Si cela se fait à la bonne fréquence, les ondes et leur réflexion interfèrent pour former des ondes stationnaires. Celles-ci sont constituées de nœuds et d’anti-nœuds.
(source: https://www.slideserve.com/deanne/wave-properties-e-m-spectrum)
Tous les nœuds restent immobiles tout au long du processus, tandis que les anti-nœuds oscillent rapidement de haut en bas. La quantité d’ondes stationnaires est directement proportionnelle à la fréquence.
Les ondes stationnaires que vous avez rencontrées en résolvant la chambre n’étaient cependant pas seulement sur une ligne unidimensionnelle, mais sur une plaque bidimensionnelle. Cette plaque est appelée plaque de Chladni. En principe, le fonctionnement est exactement le même que dans le cas unidimensionnel. Une tige placée au centre de la plaque oscille de haut en bas à une certaine fréquence. Cela génère des ondes sur la plaque. Sur le bord, elles sont encore réfléchies, comme dans le cas unidimensionnel, ce qui peut donner lieu à des ondes stationnaires. La forme de ces ondes dépend de la forme du bord de la plaque. Ces ondes stationnaires ne sont également générées qu’à certaines fréquences.
Traduit avec DeepL.com (version gratuite)
La raison pour laquelle ce concept est si important en mécanique quantique vient des mathématiques qui sous-tendent la mécanique quantique. L’ensemble du domaine repose fortement sur les mathématiques de l’algèbre linéaire. Dans ce domaine mathématique, les opérateurs, représentés par des matrices, sont d’une importance vitale, mais ils ont souvent ce que l’on appelle des valeurs propres et des vecteurs propres. Les ondes stationnaires peuvent être considérées comme les états propres de ces systèmes oscillants. Ainsi, dans une théorie reposant sur ces mathématiques, il est intuitif que ces types d’ondes jouent un rôle important.
