In one of the puzzles, you had to let a small plate of a certain material float across a train track to hit a sensor. This only worked for precisely one of the the plates, namely the one made of graphite. Some may have already guessed that magnets were at work, which is definitely the case, as the tracks are magnetic. However, simple magnetism is not sufficient. While it is simple to get one magnet to push away another, even overpowering gravity, that does not necessarily result in flotation. An additional condition is stability. If you have the chance, try to levitate one magnet on top of another. You will quickly notice that this is very hard. It is not only extremely difficult for normal magnets to result in stable floating, but it can be proven that it is impossible! Therefore, another physical concept is required, diamagnetism. This is a property that all objects have to a certain extent. It results in the material counteracting an applied magnetic field and is a result from one of Maxwell’s Equations that describe electromagnetism. It states that in response to a magnetic field, a current is established to counteract it. Since any material is partially comprised of electrons, it creates something similar. This current results in a magnetic field that counteracts the original field. Because it counteracts an external field in any direction, this process does result in in stable levitation. However, not every substance displays this effect to the same extent. In many materials, such as iron, other effects, like ferromagnetism are dominant. The amount of diamagnetism depends on the exact composition. While the precise mechanisms are complicated, generally, circular structures are beneficial, as they allow for a simpler current. Looking at the molecular structure of graphite, one can see that its crystalline structure is very circular, which is why the diamagnetic effect is particularly strong for that plate.
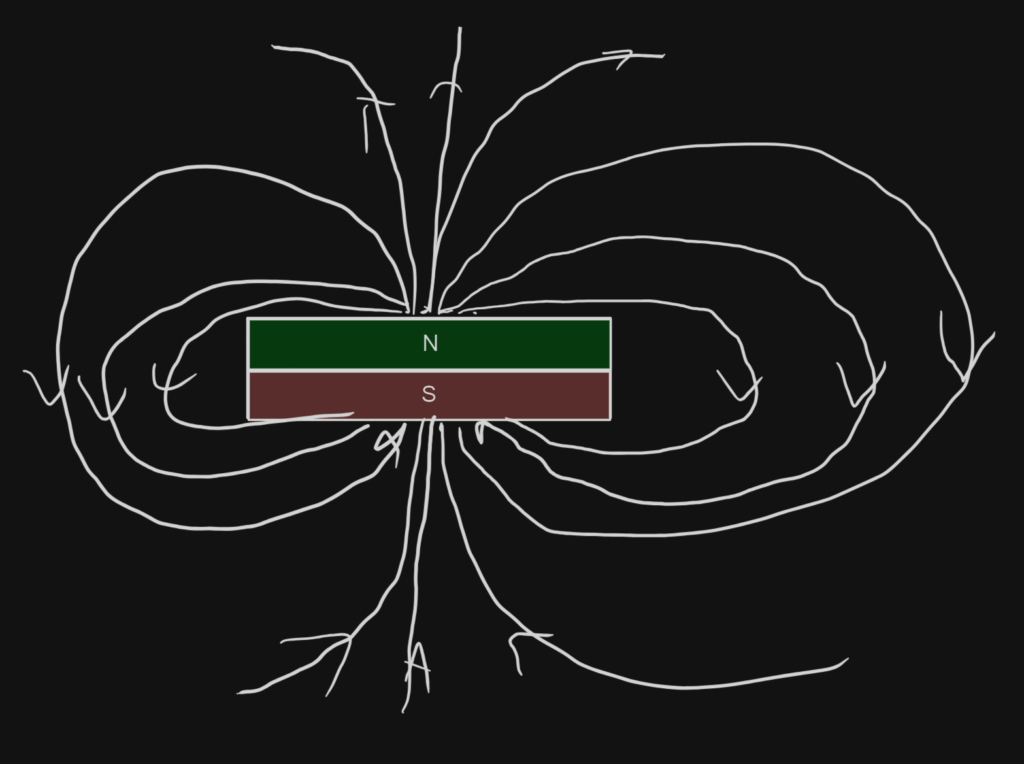
Concretely, this changes the magnetic field in a way to construct a sort of stable bubble around the plate. For that, one needs to first understand what magnetic fields look like normally. One single magnet in the the track generates a standard magnetic field, looking something like the sketch below. While it is hard to arrive at the force directly from the magnetic field to the force experienced by another magnet, generally, the denser the lines, the stronger the force. To be precise, the gradient determines the strength of the attraction.
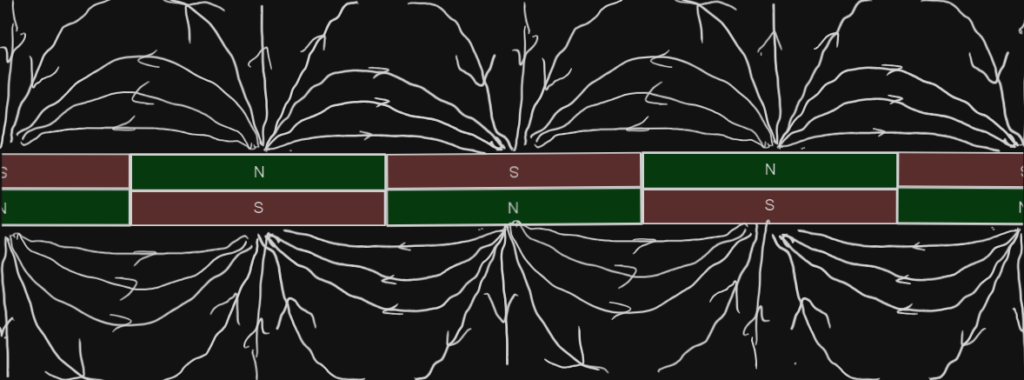
In the actual track, many of these magnets come together, alternating, which side of the magnet points upwards to ensure a stable track.
For illustration purposes only, we now assume that the magnetic field in which the plate floats to be homogenous. This is not only obviously not the fact when looking at the picture of the track above, but it wouldn’t even float in a perfectly homogenous curl. Since, as explained before, the force depends on the gradient of the magnetic field, it needs a constant amount of gradient to counteract gravity and thus float. That gradient is only given at a certain height, hence why it always flies at the same height. Moreover that is also why it likes certain positions better, as it needs to overcome slight humps. Nevertheless, these complex field lines are too complicated to draw, so we use a homogenous field to describe how the diamagnet affects the magnetic field. The top sketch is equivalent to a situation, where a coin or another none diamagnet is used.
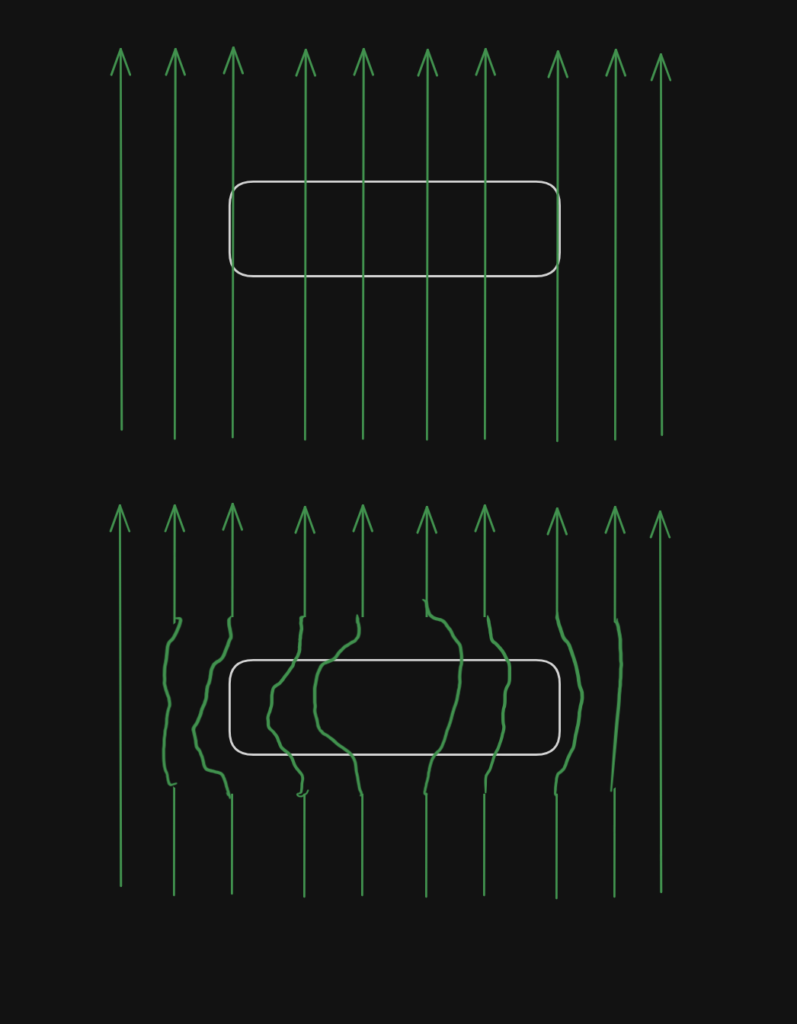
In the case of a diamagnet, the field lines are bent around it a little, as seen in the bottom image this creates a stable pocket, where the plate can float in a stable manor. Of course, all of this is only a simplification, as edge effects have been ignored and as stated previously, the real field is not homogenous. It is very hard to understand this concept thoroughly, as it requires a large amount of knowledge on magnetism generally. The following resources can be helpful to build an understanding:
Magnetism and electromagnetism | AP®︎/College Physics 2 | Khan Academy
