Ein wichtiges Konzept in der Quantenphysik sind stehende Wellen. Sie helfen bei der Beschreibung einer Vielzahl von Phänomenen, die Physiker nur schwer klassisch erklären konnten. Dazu gehören die bereits erwähnte Schwarzkörperstrahlung oder die Umlaufbahn von Elektronen. Es ist zwar zu kompliziert, hier zu erklären, wie genau sie in der Quantenmechanik verwendet werden, aber das allgemeine Konzept und warum sie wichtig sind, kann erklärt werden. Zunächst einmal ist das allgemeine Konzept der stehenden Wellen relativ leicht zu verstehen. Wenn man eine Schnur hat und eine Welle hinunterschickt, wird sie schließlich zurückreflektiert. Wenn dies mit der richtigen Frequenz geschieht, überlagern sich die Wellen und ihre Reflexion und es entstehen stehende Wellen. Diese bestehen aus Knoten und Wellenbäuche.
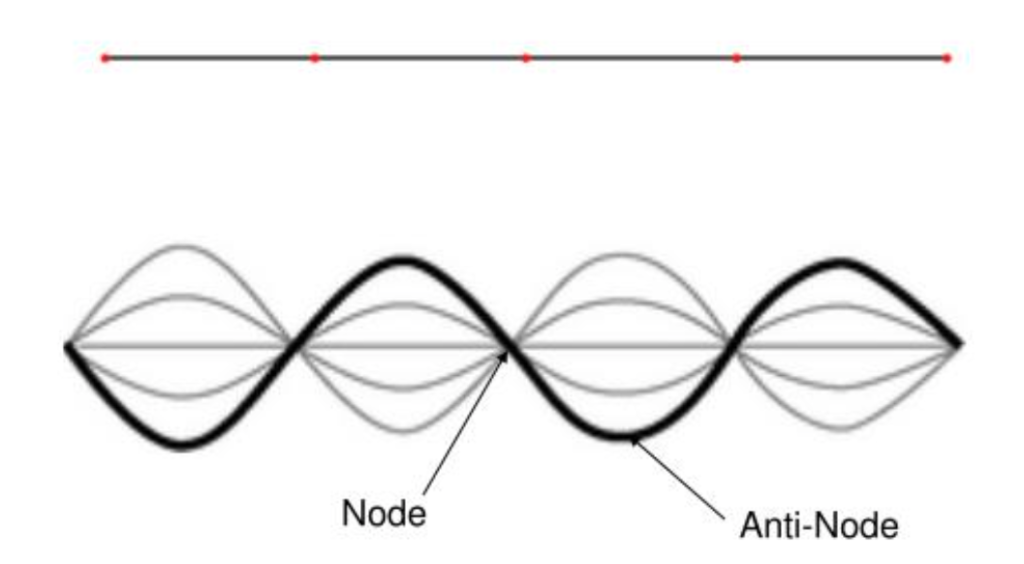
Alle Knotenpunkte bleiben während des gesamten Prozesses unverändert, während die Wellenbäuche schnell auf und ab schwingen. Die Menge der stehenden Wellen ist direkt proportional zur Frequenz.
Die stehenden Wellen, auf die Sie bei der Lösung des Raumes gestoßen sind, befanden sich jedoch nicht nur auf einer eindimensionalen Linie, sondern auf einer zweidimensionalen Platte. Diese Platte wird Chladni-Platte genannt. Im Prinzip funktioniert sie aber genauso wie im eindimensionalen Fall. Ein Stab in der Mitte der Platte wird mit einer bestimmten Frequenz auf und ab geschwungen. Dadurch werden auf der Platte Wellen erzeugt. Am Rand werden sie wie im eindimensionalen Fall immer noch reflektiert, was zu stehenden Wellen führen kann. Die Form dieser Wellen hängt von der Form des Plattenrandes ab. Auch diese stehenden Wellen werden nur bei bestimmten Frequenzen erzeugt.
Der Grund, warum dies ein so wichtiges Konzept in der Quantenmechanik ist, liegt in der Mathematik, die der Quantenmechanik zugrunde liegt. Das gesamte Gebiet stützt sich stark auf die Mathematik der linearen Algebra. In diesem Bereich der Mathematik sind Operatoren, die durch Matrizen dargestellt werden, von entscheidender Bedeutung; diese haben jedoch oft etwas, das Eigenwerte und Eigenvektoren genannt wird. Stehende Wellen können als Eigenzustände dieser schwingenden Systeme betrachtet werden. In einer Theorie, die sich auf diese Mathematik stützt, ist es daher intuitiv, dass diese Arten von Wellen eine wichtige Rolle spielen.
